Вперше в житті мені стала в пригоді тригонометрія. Чекав цього ще з часів школи :)
Зараз працюю над новими дорожніми знаками (деталі тут), і коли йшла робота над знаками напрямку повороту, хотілося наочно побачити, як вони будуть виглядати з різним кутом шевронної стрілки.
Розкажу, як це зробити. Спочатку треба підготувати зображення знаку у форматі SVG:
Це зображення — лише відтворення такого коду:
<svg width="1115" height="230" viewBox="0 0 1115 230" fill="none" xmlns="http://www.w3.org/2000/svg">
<g clip-path="url(#mask)">
<rect width="1115" height="230" fill="#DA0000" />
<path id="path-1" d="M120 0L235 115L120 230" stroke="white" stroke-width="77" stroke-linecap="square" />
<path id="path-2" d="M394 0L509 115L394 230" stroke="white" stroke-width="77" stroke-linecap="square" />
<path id="path-3" d="M668 0L783 115L668 230" stroke="white" stroke-width="77" stroke-linecap="square" />
<path id="path-4" d="M942 0L1057 115L942 230" stroke="white" stroke-width="77" stroke-linecap="square" />
</g>
<defs>
<clipPath id="mask">
<rect width="1115" height="230" fill="white" />
</clipPath>
</defs>
</svg>
Цей код можна пояснити так:
- маємо полотно розміром 1115×230 пікселів,
- на цьому полотні є червоний прямокутник на всю ширину і висоту,
- і чотири білих стрілки товщиною 77 пікселів,
- є також маска, щоб не дати контурам стрілок вийти за межі прямокутника, але про це наразі можна не думати.
Складно виглядає це M120 0L235 115L120 230, але насправді все не так страшно. M означає Move to — це команда йти в точку (120,0). Далі L (Line to) — малюй лінію з попередньої точки в точку (235,115), а потім продовжуй лінію в точку (120,230).
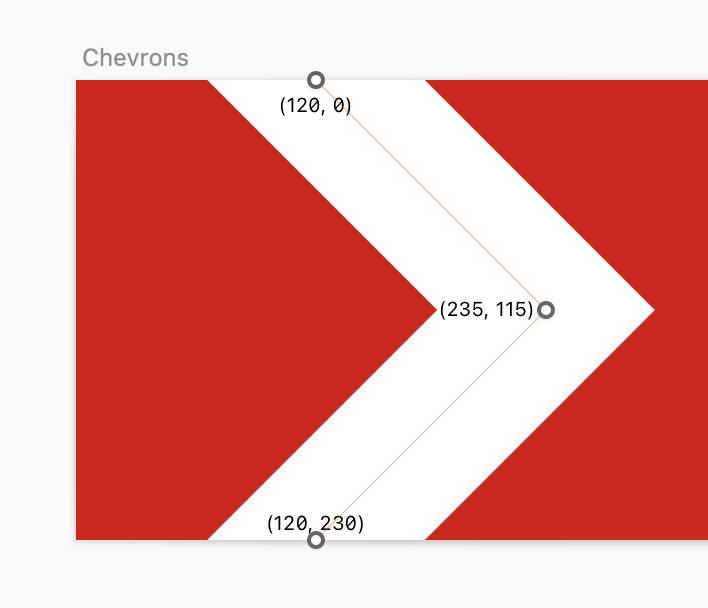
Ми можемо змінювати координати точок, керуючи SVG-кодом за допомогою JavaScript. Але спочатку треба зрозуміти, як саме це зробити.
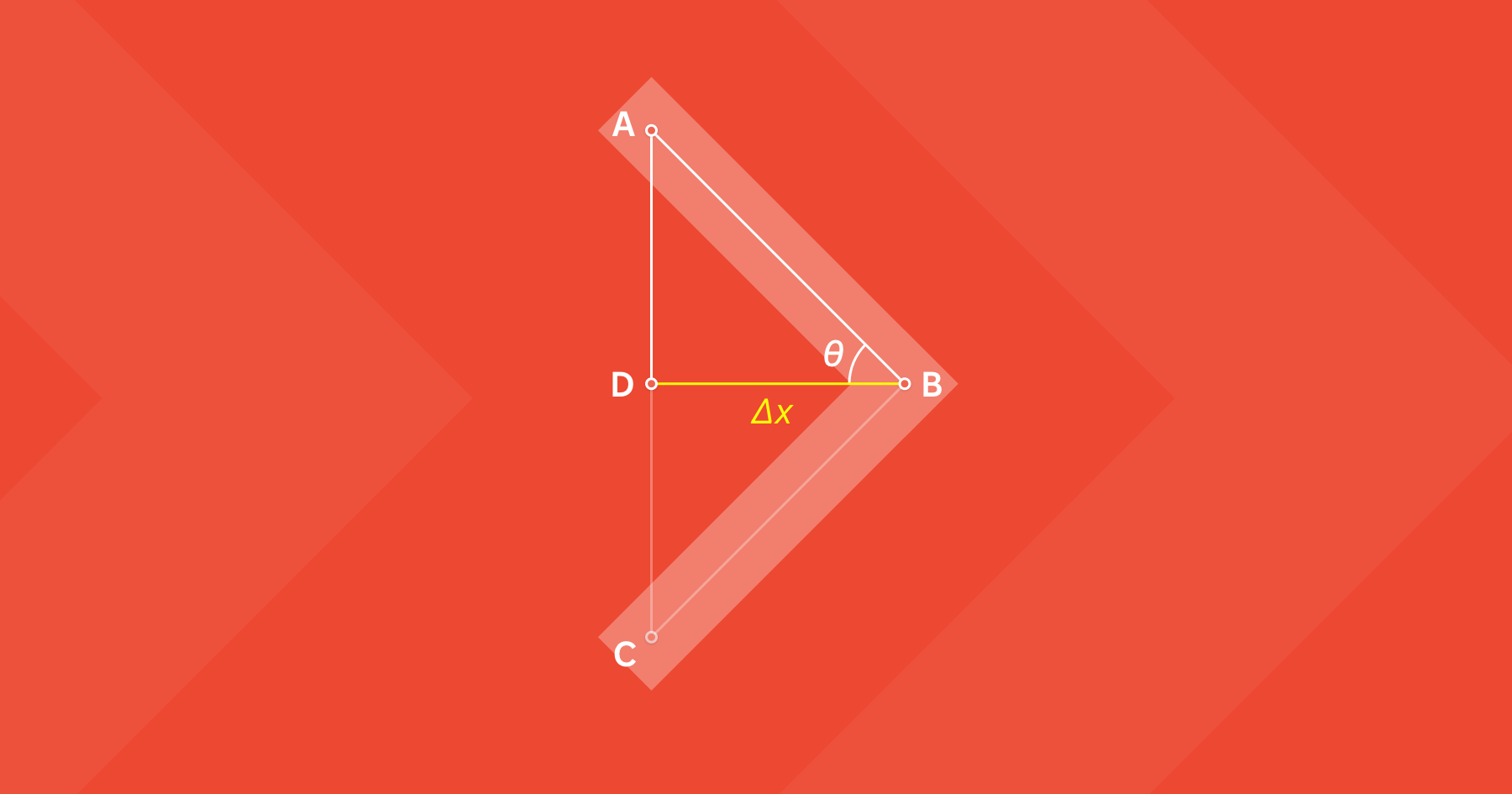
Отже, ми хочемо задати певний кут у градусах і визначити відстань, на яку потрібно змістити центральну точку по горизонталі, щоб величина кута була саме такою, яку ми задамо.
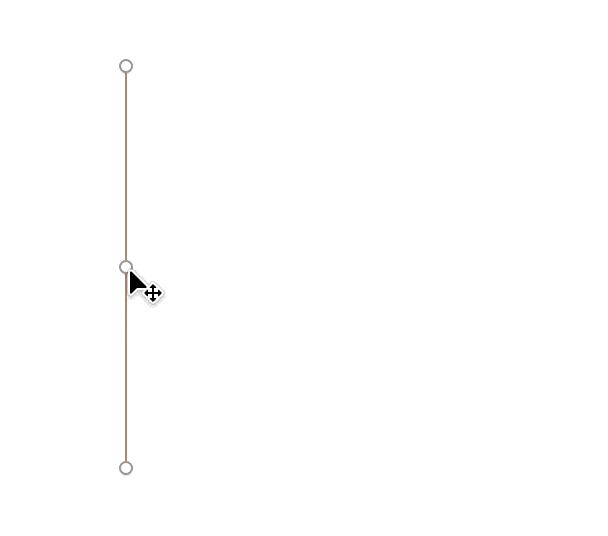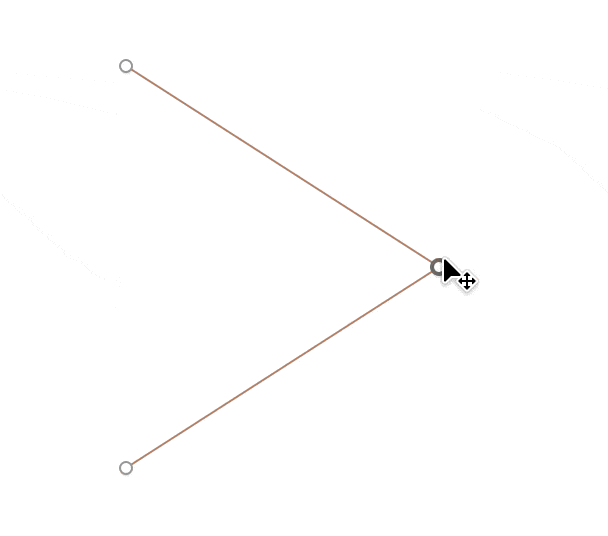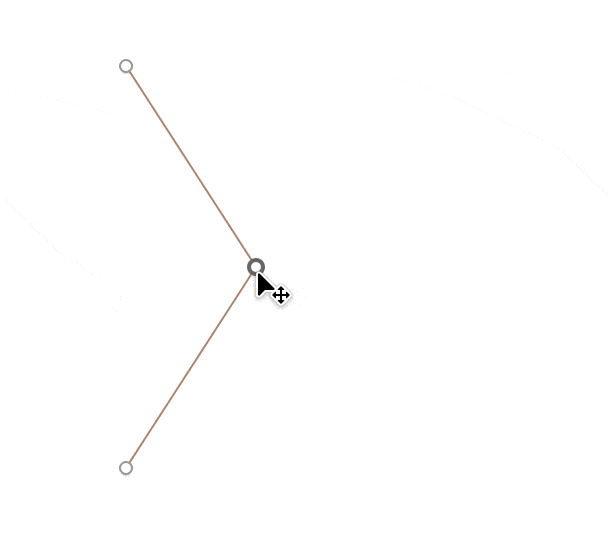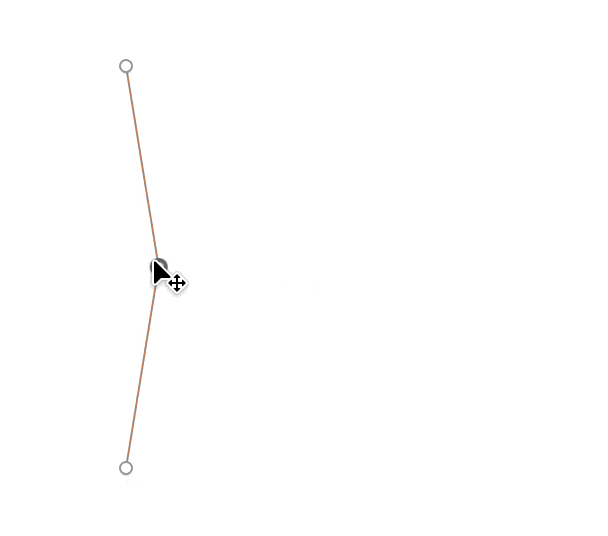
Намалюємо трикутник ABC. Розділимо його навпіл лінією Δx — саме цю довжину нам треба буде шукати. Позначимо кут θ, який буде завжди дорівнювати половині заданого кута. Тепер можемо працювати з прямокутним трикутником ABD:
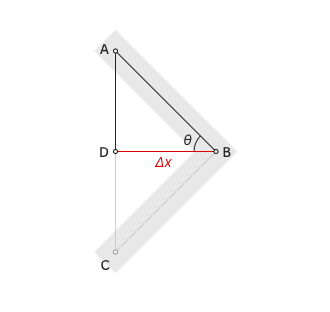
Відстань AC — постійна (230 пікселів на нашій картинці). AD дорівнює половині AC.
Знаючи величину кута θ і довжину однієї сторони, ми можемо знайти довжину іншої сторони. З цим допоможе тангенс кута θ: він показує відношення протилежної сторони AD до прилеглої сторони Δx:
Знайдемо звідси Δx:
Підставимо у формулу відомі нам значення (AD = AC ÷ 2; β — заданий кут):
В JavaScript це буде виглядати так:
const height = 230; // Висота `AC`
angleSlider.addEventListener('input', function () {
const angle = parseInt(this.value);
const radians = angle * Math.PI / 180; // JS потребує значення кута в радіанах
const deltaX = height / (2 * Math.tan(radians / 2));
// Працюємо з координатами для кожної стрілки
chevronPaths.forEach((path, index) => {
const { x } = defaultPositions[index];
const middleX = x + deltaX;
// ...і передаємо їх в SVG
path.setAttribute('d', `M${x} 0L${middleX} 115L${x} 230`);
});
});
Працює! Можна тестувати. І хоч зрештою ми залишили на стрілках кут 90°, як на поточних знаках, поекспериментувати було дуже цікаво.
Ви можете подивитись на те, що у нас вийшло з шевронними знаками у блозі «Попереду нові дорожні знаки».
Бонус: що я дізнався, поки працював над цим знаком
- Щоб отримати прямий кут, достатньо змістити центральну точку рівно на половину висоти стрілки.
- В JavaScript є тангенс, але немає котангенсу. Щоправда, котангенс було б легко розрахувати, розділивши одиницю на тангенс.
- А ще я нагадав собі, як приємно працювати над дизайном і кодом, взагалі не думаючи про конверсії та бізнес-показники 💆♂️. Відкалібрував свій компас.